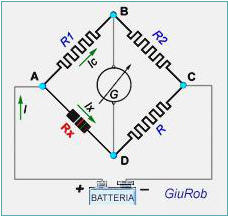
Il Ponte di Wheatstone è tilizzato per misurare con precisione resistenze di valore compreso tra 1 Ohm e 100 Kohm. (per le resistenze con valori bassi inferiore a 1 Ohm si usa il "Doppio Ponte di Thomson") L’elemento Rx rappresenta la resistenza di valore incognito da misurare. Gli elementi R, R1 e R2 sono resistenze, dette di taratura, variabili e di valore noto. Nei punti A e C si applica la tensione d’alimentazione. E’ importante precisare che, per questo metodo di misura relativo alle resistenze, la tensione deve essere continua; ovvero, deve avere le caratteristiche di quella fornita dalle batterie. Nei punti B e D s’inserisce uno strumento di misura, molto sensibile, detto Galvanometro a zero centrale. Esso ha la funzione di indicare quando il ponte è in equilibrio: condizione indispensabile per la misura della resistenza incognita. Il ponte è in equilibrio, se il galvanometro indica zero, ossia NON è percorso da corrente. Questo avviene se il potenziale elettrico del punto B è uguale a quello del punto D.  ovvero: Vb = Vd [e].  L'equilibrio del ponte si ottiene variando opportunamente le resistenze R, R1 e R2. Una volta effettuata la taratura, e noti i valori delle tre resistenze, si calcola il valore di Rx con la seguente relazione: Rx = (R1 / R2) * R  

Ponte di Wheatstone un esempio pratico a cura di Giuliano D. (GiuRob)

Dimostrazione Se il ponte di Wheatstone è in equilibrio le resistenze R1 e R2 sono attraversate dalla stessa corrente Ic  mentre le resistenze Rx e R sono attraversate dalla stessa corrente Ix Per la Legge di Ohm si può scrivere: Va - Vb = R1 * Ic [a] Va - Vd = Rx * Ix [b] Vb - Vc = R2 * Ic [c] Vd - Vc = R * Ix [d] Tenendo presente la relazione [e], possiamo sostituire: Vb con Vd nella formula [a] Vd con Vb nella formula [d] Ottenendo: Va - Vd = R1 * Ic Va - Vd = Rx * Ix Vd - Vc = R2 * Ic Vd - Vc = R * Ix quindi: R1 * Ic = Rx * Ix R2 * Ic = R * Ix dividendo membro a membro si ottiene: R1 / R2 = Rx / R da cui: Rx = (R1 / R2) * R come volevasi dimostrare

Ponte di Wheatstone